
Exact Science
@exscicoLondon-based school specialising in Olympiad Mathematics and Programming | AI-resistant problems are posted daily!
Problem of the Day #143: For how many three-digit numbers can you subtract 297 and obtain a second three-digit number which is the original three-digit number reversed? The solution link is in the bio. #NumberTheory #ThreeDigitNumbers #ProblemSolving #PlainText #Mathematics

Problem of the Day #142: Two of the following four facts about a positive integer N are true and two are false: What is the value of N? The solution link is in the bio. #Divisibility #IntegerProperties #ProblemSolving #PlainText #Mathematics

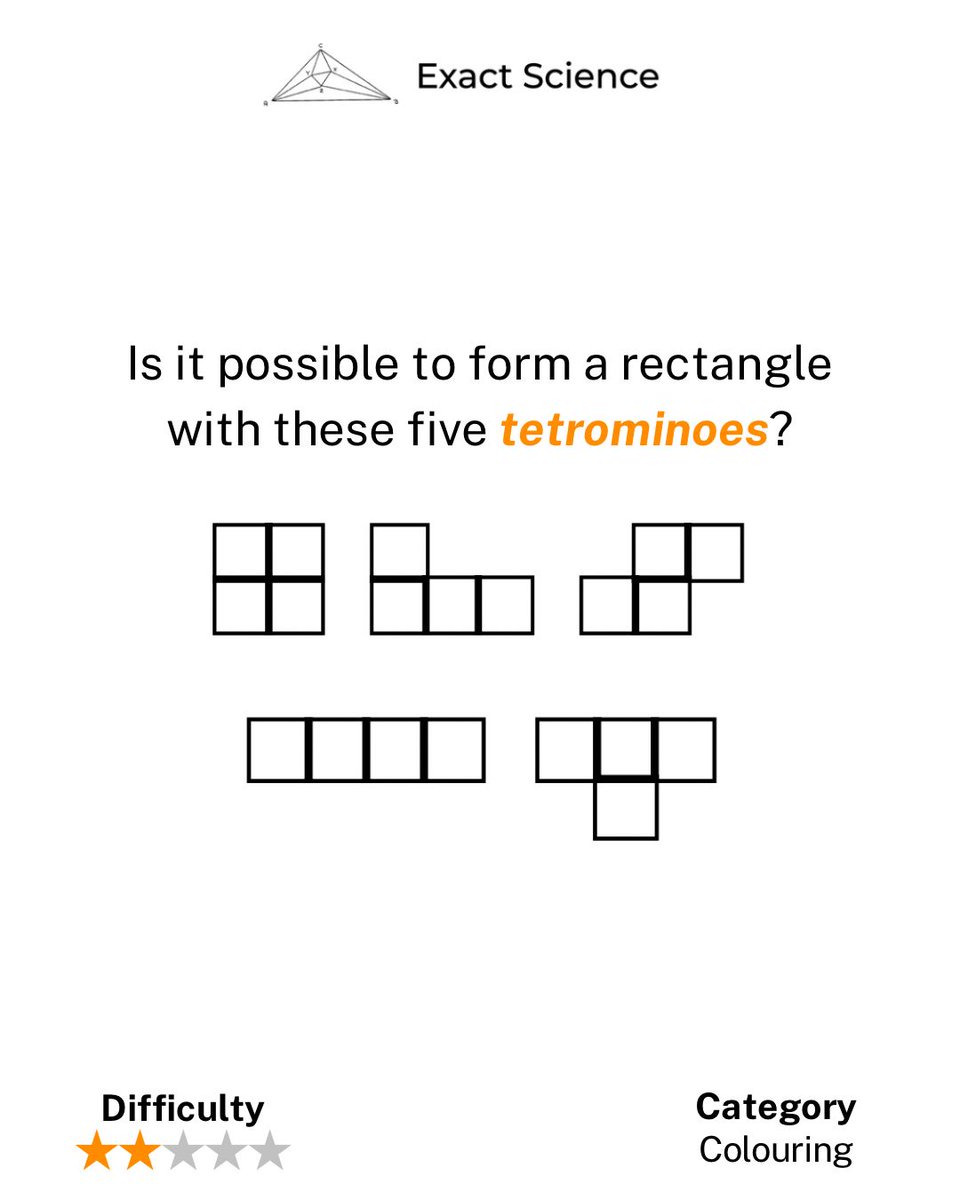
Problem of the Day #141: Is it possible to form a rectangle with these five tetrominoes? The solution link is in the bio. #Tetrominoes #RectangleFormation #ProblemSolving #Colouring #Mathematics
Problem of the Day #140: The numbers 1, 2, 3, 4, and 5 are used once each in some order substituting for the letters in the series of powers. In how many of the arrangements is the units digit of the value of this expression equal to 1? Source: Hamilton - 2024 - 4 #ExactScience

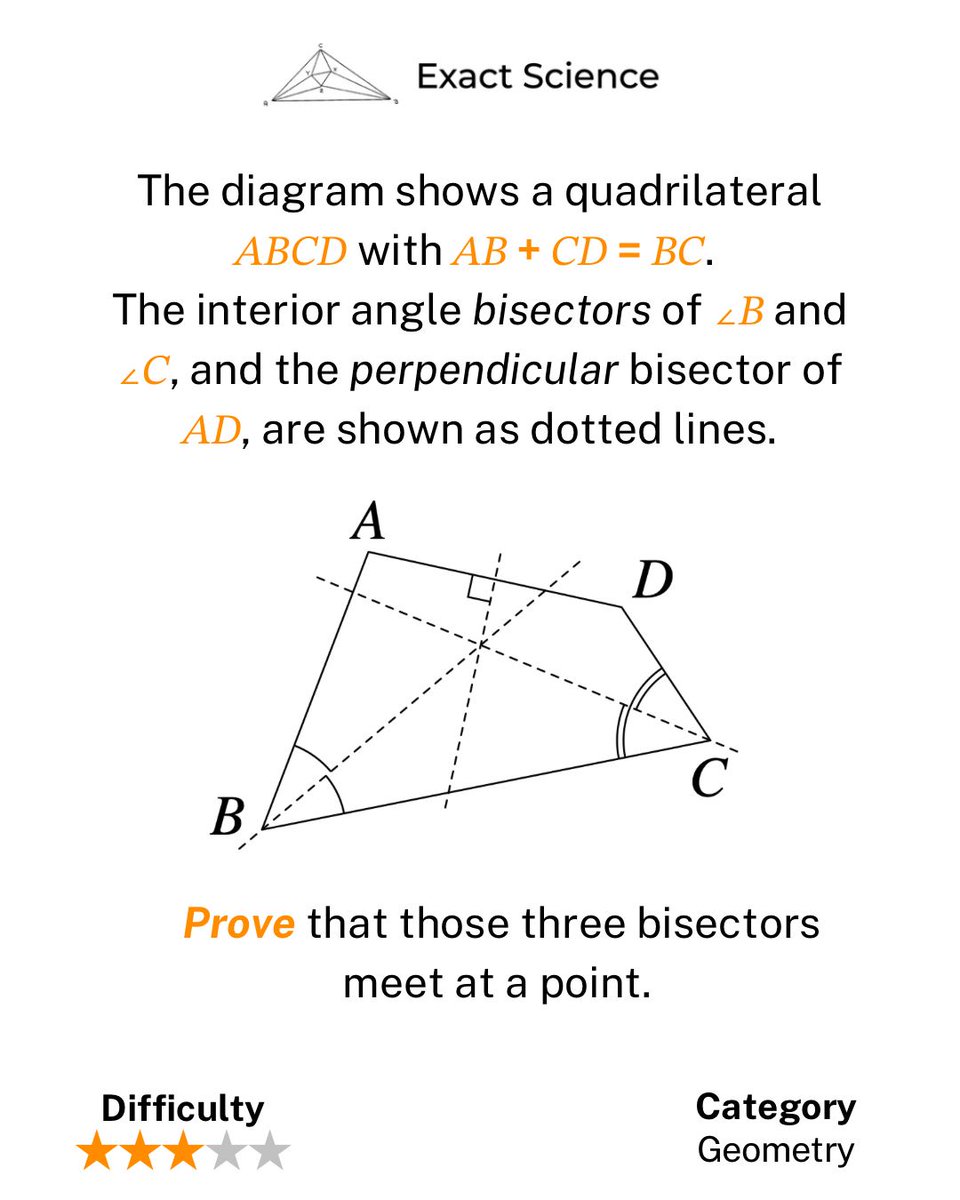
Problem of the Day #139: Source - Intermediate Mathematical Olympiad - Hamilton Paper - 2024 - 6 The solution link is in the bio. #GeometryProblem #BisectorsIntersection #ProblemSolving #PlainText #Mathematics
Problem of the Day #138: Source: Intermediate Mathematical Olympiad - Cayley Paper - 2024 - Q5 The solution link is in the bio. #GroupSize #MeanValue #ProblemSolving #Mathematics

Problem of the Day #137: A positive integer N < 2024 is divisible by 39 times the sum of its digits. Find all possibilities for N. The solution link is in the bio. #NumberTheory #Divisibility #ProblemSolving #PlainText #Mathematics

Problem of the Day #136: PQRST is a regular pentagon. The point U lies on ST such that ∠QPU is a right angle. What is the ratio of the interior angles in triangle PUT? The solution link is in the bio. #GeometryProblem #RegularPentagon #AngleRatio #ProblemSolving #Mathematics

Problem of the Day #135: Wenlu, Xander, Yasser, and Zoe make the statements. What are the possible numbers of people telling the truth? The solution link is in the bio. #LogicPuzzle #TruthTellers #ProblemSolving #Mathematics

Problem of the Day #134: Source: UKMT - Cayley Olympiad - 2022 - 5 The solution link is in the bio. #Algebra ProblemSolving #Mathematics

Problem of the Day #133: Source: UKMT - Cayley Olympiad - 2023 - 5 The solution link is in the bio. #NumberTheory #PrimeFactors #ProblemSolving #Mathematics

Problem of the Day #132: Consider all 100-digit positive integers such that each decimal digit of these equals 2, 3, 4, 5, 6, or 7. How many of these integers are divisible by 2^100? Source: Tournament of Towns - O-Level - Fall - 2023 - 4 #NumberTheory #Divisibility #Mathematics

Problem of the Day #131: One of the students from class A was transferred to class B, which increased the average height of students in both classes. Could this be possible? The solution link is in the bio. #AverageHeight #Transfer #ProblemSolving #Mathematics

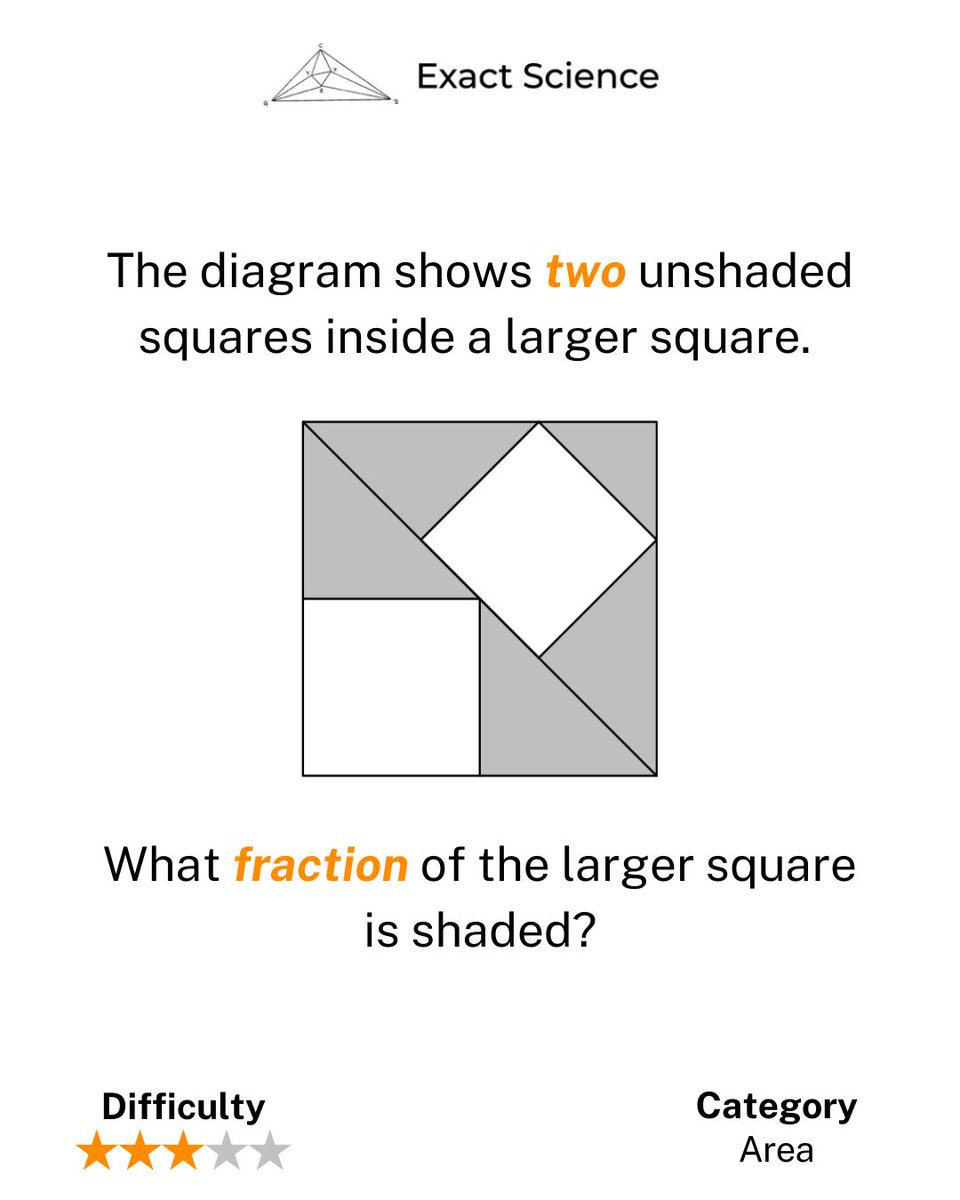
Problem of the Day #130: The diagram shows two unshaded squares inside a larger square. What fraction of the larger square is shaded? The solution link is in the bio. #GeometryProblem #FractionCalculation #ProblemSolving #PlainText #Mathematics
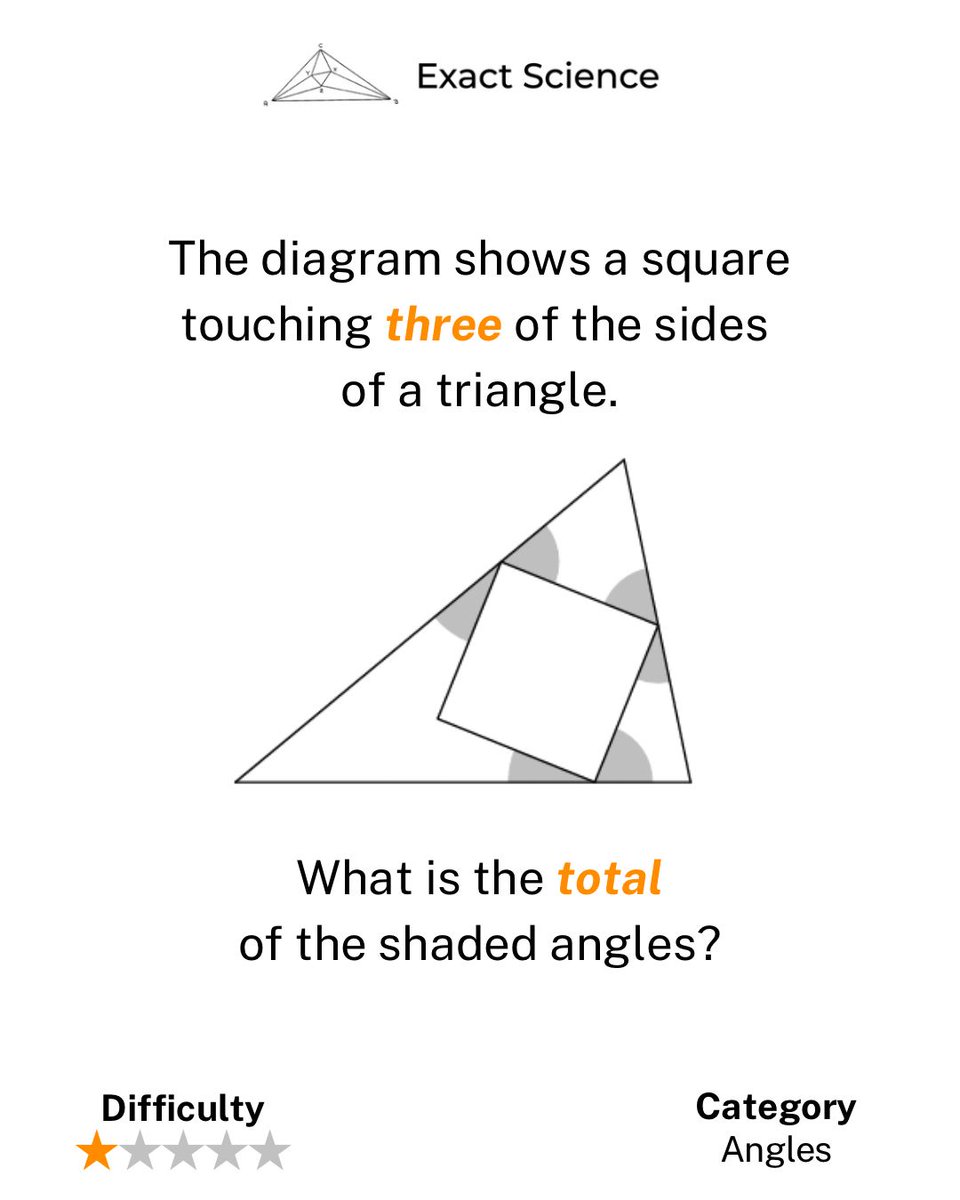
Problem of the Day #129: The diagram shows a square touching three of the sides of a triangle. What is the total of the shaded angles? The solution link is in the bio. #GeometryProblem #AngleCalculation #ProblemSolving #PlainText #Mathematics
Problem of the Day #128 The solution link is in the bio. #NumberManipulation #BlackboardProblem #ProblemSolving #PlainText #Mathematics

Problem of the Day #127: Given four integers a, b, c, and d such that a + b + c + d = ab + bc + cd + da + 1, prove that the absolute values of two of these numbers differ by one. The solution link is in the bio. #IntegerEquation #AbsoluteValue #ProblemSolving #Mathematics
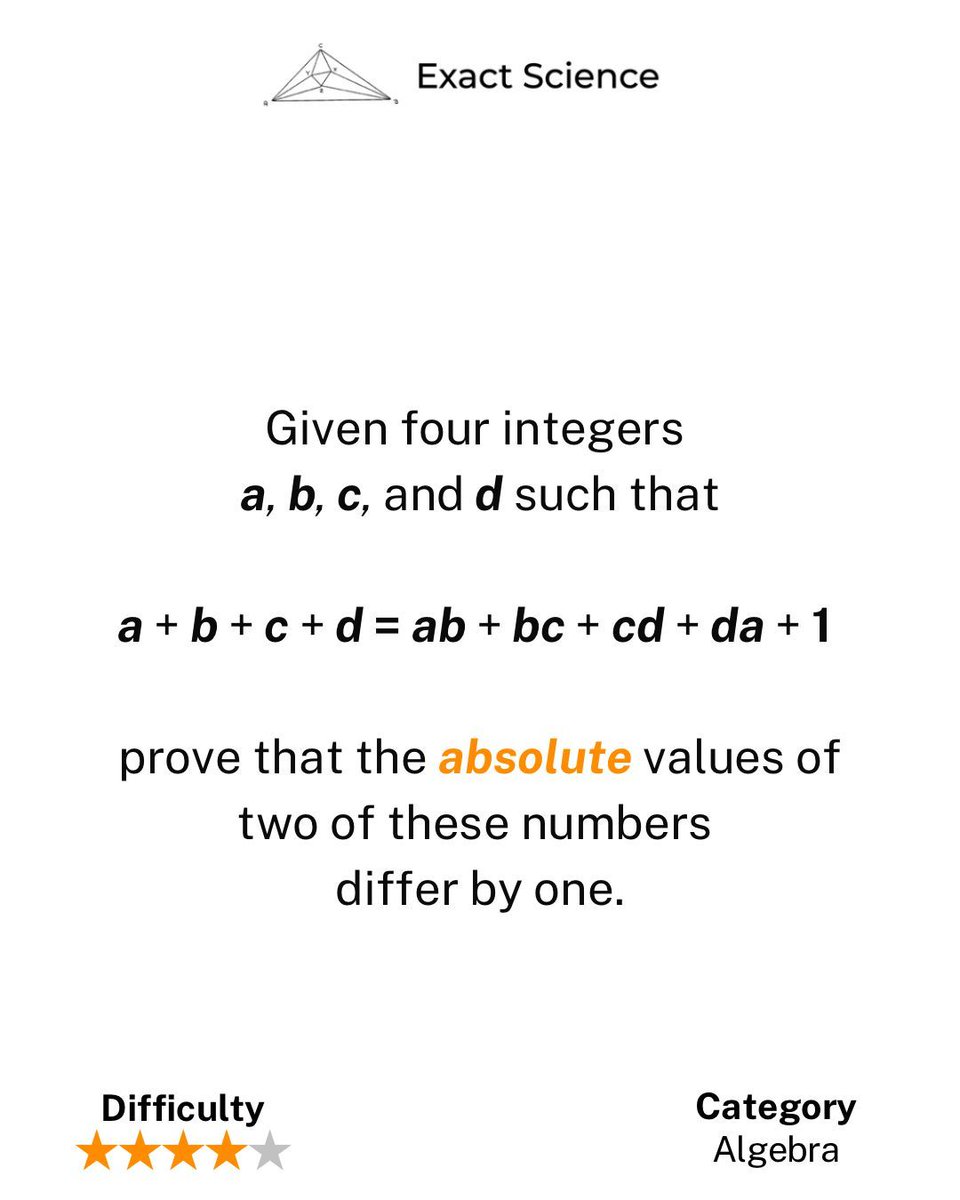
Problem of the Day #126: Prove that among the powers of two, there exist two whose difference is divisible by 2024. The solution link is in the bio. #NumberTheory #PowersOfTwo #Divisibility #ProblemSolving #Mathematics

Problem of the Day #125: Note that the value of 1!·1 + 2!·2 + 3!·3 + ... + n!·n is equal to 1, 5, 23, 119 for n = 1, 2, 3, 4 respectively. Determine the general rule and prove it. The solution link is in the bio. #NumberSequence #ProblemSolving #ExactScience #Mathematics

Problem of the Day #124: Do there exist three different natural numbers a, b, and c, such that the numbers a + b + c and a × b × c are squares of some natural numbers? The solution link is in the bio. #NumberTheory #DiophantineEquation #ProblemSolving #ExactScience #Mathematics

United States Trends
- 1. Mike 1,83 Mn posts
- 2. Serrano 239 B posts
- 3. Canelo 16,6 B posts
- 4. #NetflixFight 72,3 B posts
- 5. Father Time 10,8 B posts
- 6. #netflixcrash 15,8 B posts
- 7. Logan 78,8 B posts
- 8. He's 58 25,9 B posts
- 9. Rosie Perez 14,9 B posts
- 10. ROBBED 102 B posts
- 11. Boxing 300 B posts
- 12. Shaq 16,2 B posts
- 13. #buffering 10,9 B posts
- 14. My Netflix 83,2 B posts
- 15. Roy Jones 7.175 posts
- 16. Tori Kelly 5.246 posts
- 17. Ramos 69,9 B posts
- 18. Muhammad Ali 18,4 B posts
- 19. Cedric 22 B posts
- 20. #netfilx 5.056 posts
Something went wrong.
Something went wrong.






















































































