Segar Rogers
@SegarRogersSecondary maths teacher. Old enough to remember chalk.
Similar User

@draustinmaths

@mrsouthernmaths

@ChrisMcGrane84

@JaggersMaths

@DrRowlandson

@WRMathsSec

@alcmaths

@nathanday314

@blatherwick_sam

@Avi_Maths

@taylorda01
@TLMaths
@MathsPadNicola

@FortyNineCubed

@hartmaths
Crazy thought-experiment. Take a class and teach them: • quotative and partitive division concepts ... but teach them to write 12 ÷ 3 as 3 ÷ 12, mirroring the linguistic order of '3s into 12'. Would quotative strategies dominate their thinking? Crazy ;-)
Why are pupils so inclined to divide partitively rather than quotatively? The latter rarely crosses their mind … hence why 6 ÷ ¼ is deemed hard. Is it linguistic? (‘6 divided BY 2’ vs ‘2 divided INTO 6’?) … and semiotically the ÷ symbol in 6 ÷ 2 attaches itself to the former?
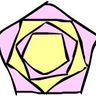
Set a timer. Put these in area order. Largest to smallest. Stop the timer. Justify your order.
Still struggling with the ugly black X icon. Going to BlueSky for a while to see what the weathers like. @segarrogers.bsky.social
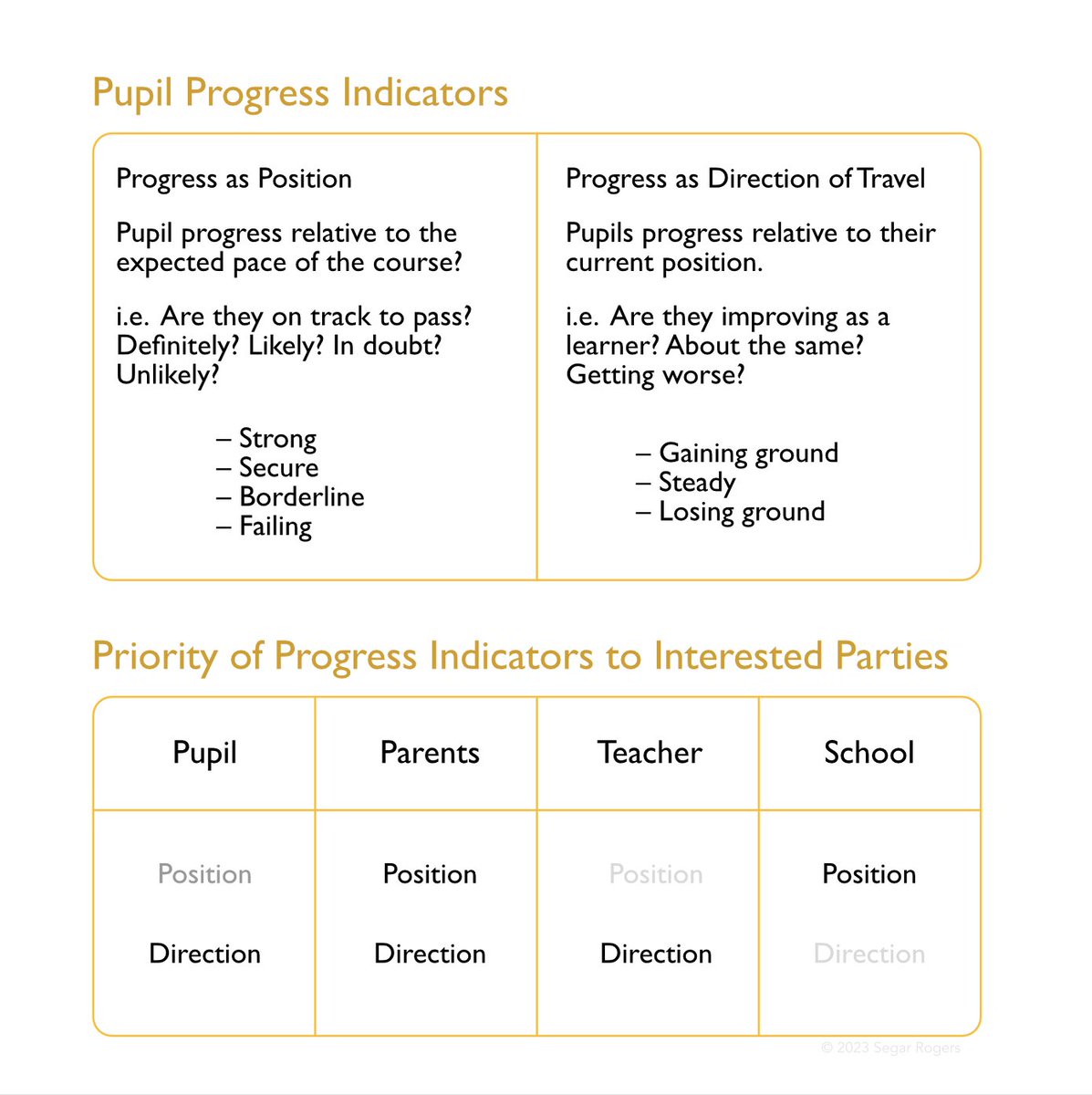
Trying to build a definition for 'progress' on pupil tracking reports . Considering dual indicators as a solution. This is me just playing with ideas. Aware some of it may be contentious. Would welcome robust criticism. @ChrisMcGrane84 @AndyBrown314 @garyl82 @mcnally_gerry

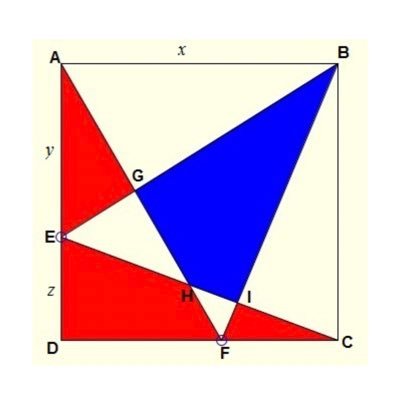
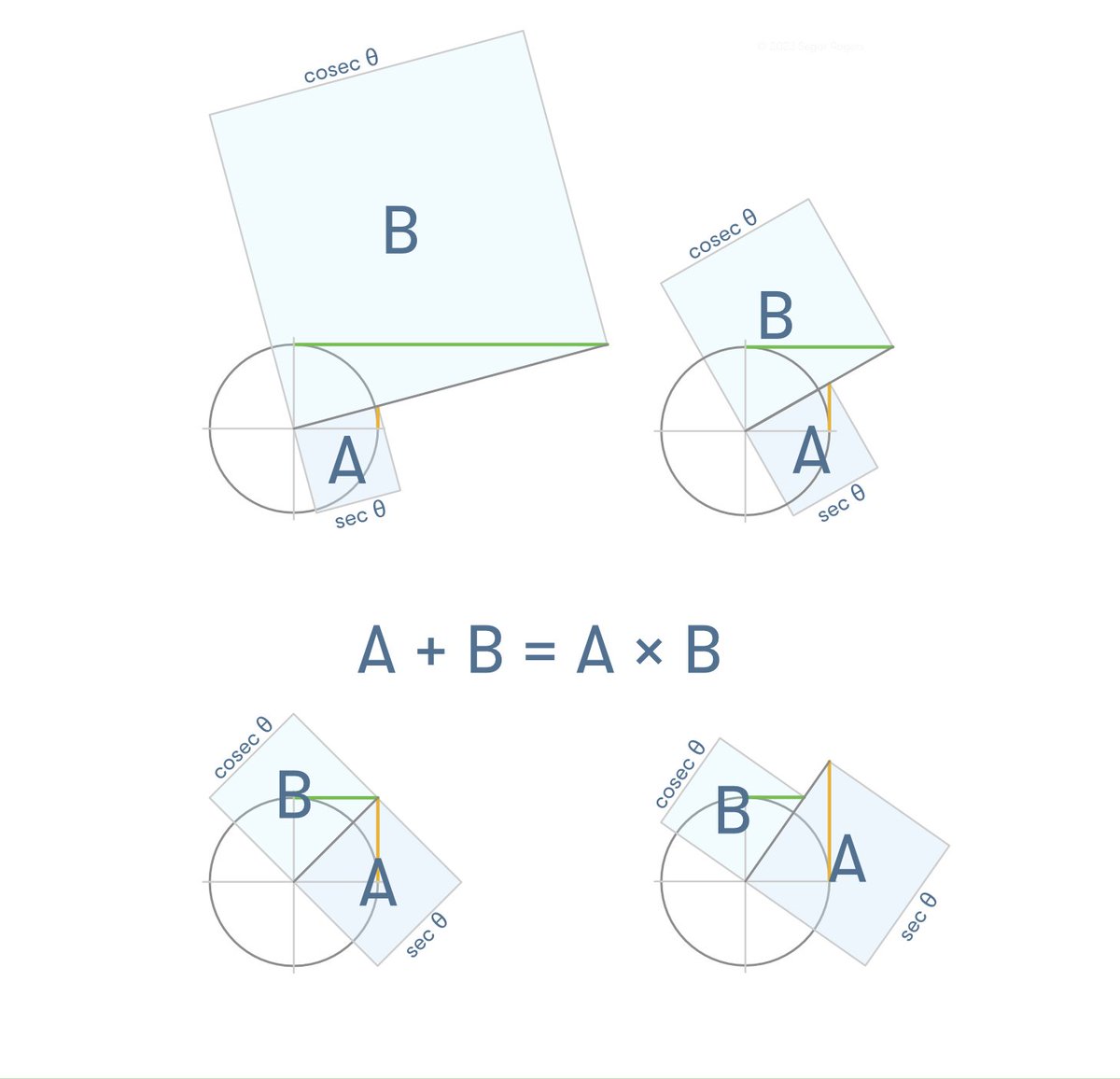
Graphical constructions of areas that satisfy the condition A + B = A × B i.e. the identity sec² θ + cosec²θ ≡ sec² θ × cosec²θ Bottom left represents A=2, B = 2. @catrionateaches @mcconvillemaths
A surprising identity in @catrionateaches tweet. Suggests maybe the following pupil task: ‘Try and find as many pairs of numbers such that a + b = a × b’ A possible prompt just as the class gives up: 6 and 1⅕ ?
I spent a lot of time modelling how I wanted Y13 to set out their ‘show that’ questions. With one class, we immediately did some practice that I live-marked, and all but one student was setting it out perfectly. With another, I set the practice as homework, due today…

I keep looking that this. 'What fraction is shaded?' What education system builds you into the person that puts a 2 on the bottom edge with the foresight that it will end so well?!
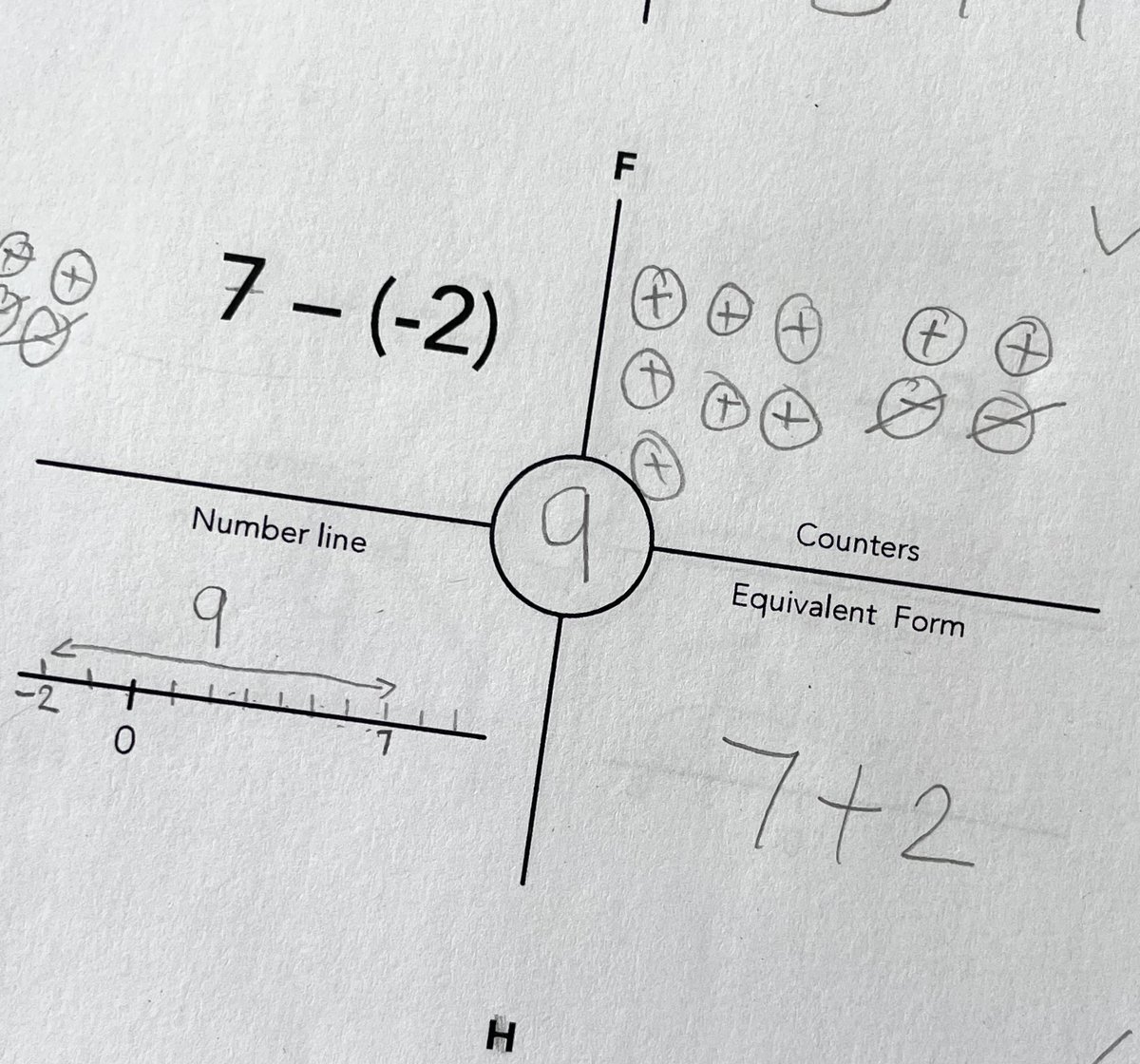
⊕⊖ zero-pairs alongside a subtraction-as-difference model. S1 were happily engrossed in this today :-) (I always feel subtraction-as-difference is under-developed in pupils … their tendency is to count-back … which is no help in this scenario).
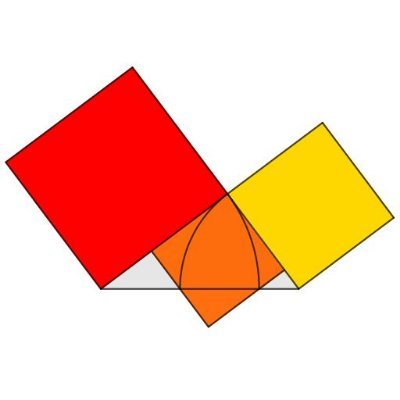
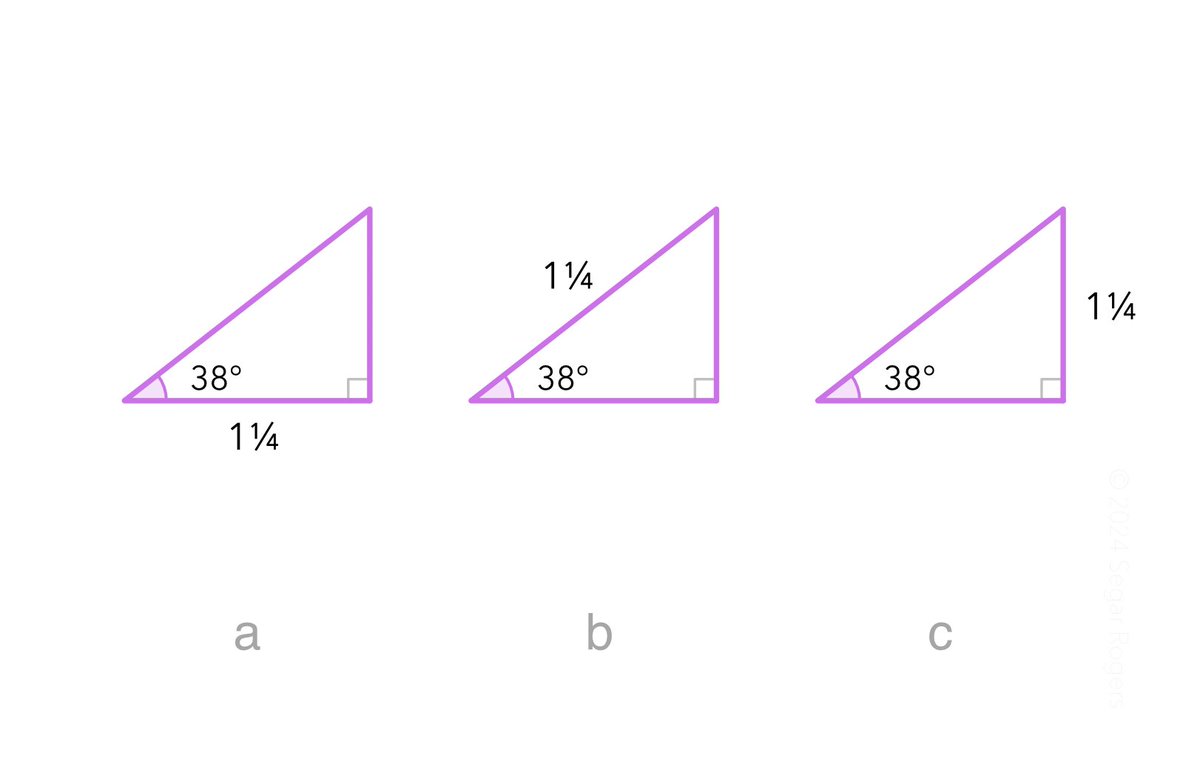
1931 Scottish Lower Grade, Paper 2. Try solving it without any algebraic manipulation or quadratic wizardry ;-) Some people will maybe just see it. @mrallanmaths
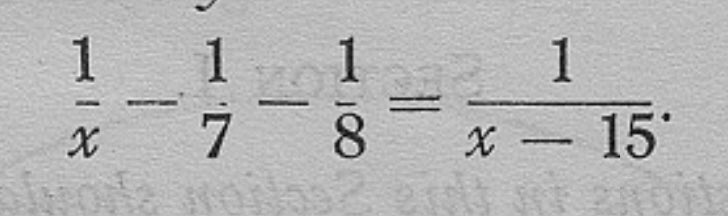
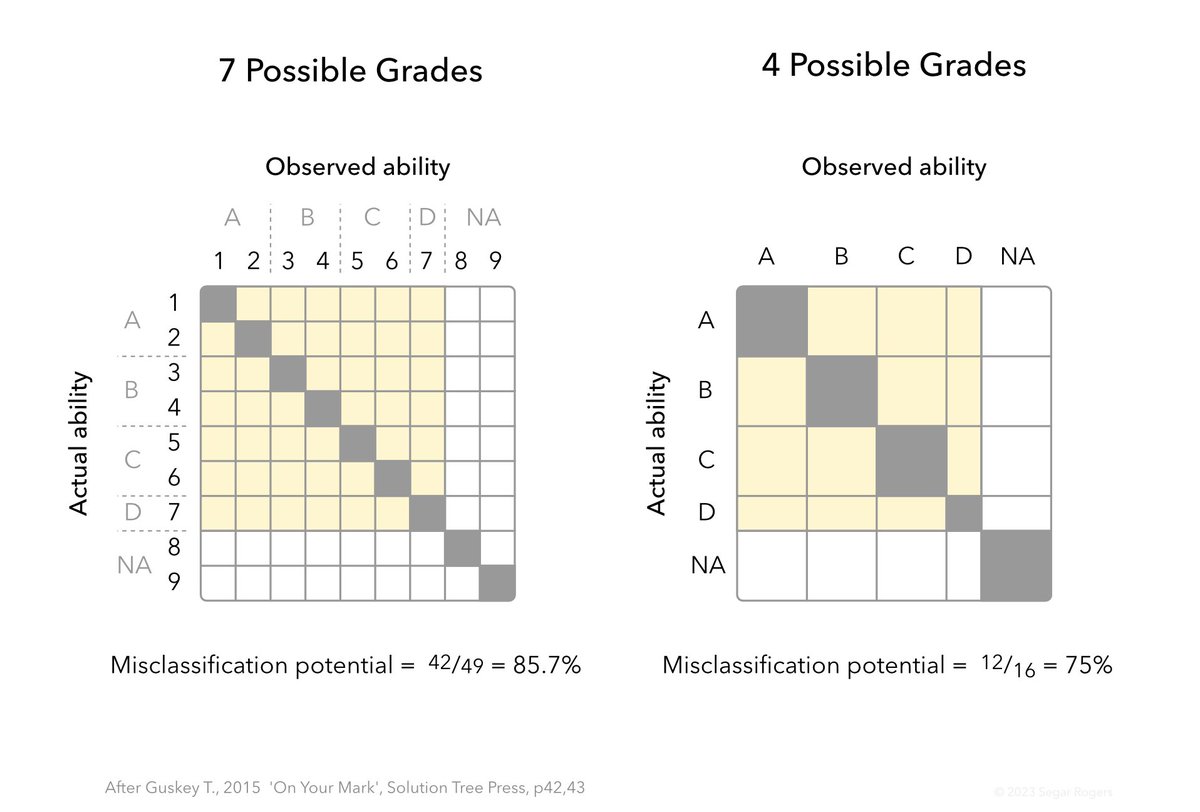
Reading Guskey about reporting in 'On Your Mark'. In my school we report using 7 possible grades (1-7). Guskey argues that if you reduce that to 4 grades (A-D) you reduce the potential for misclassification. I see it … but equally I wonder if there's a flaw in the argument.
Thinking again about Tracking & Reporting. Does anyone work in a school that reports on the impact of mobile phones in class in their pupil reports? Good idea? Bad idea? Pros? Cons?

Continued fractions with the new S2. Once you get into a rhythm they’re actually very doable … it’s just the same process iterated. One pupil did all of them in his head :-)
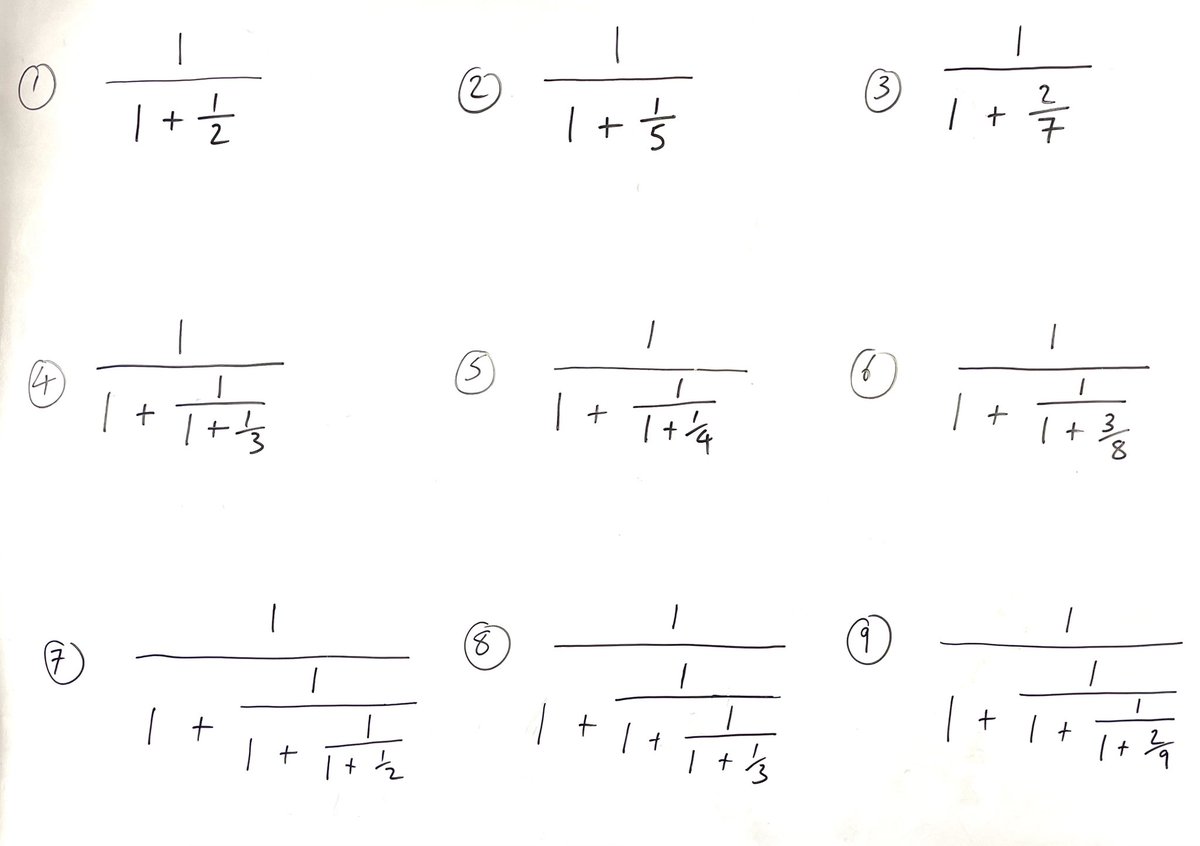
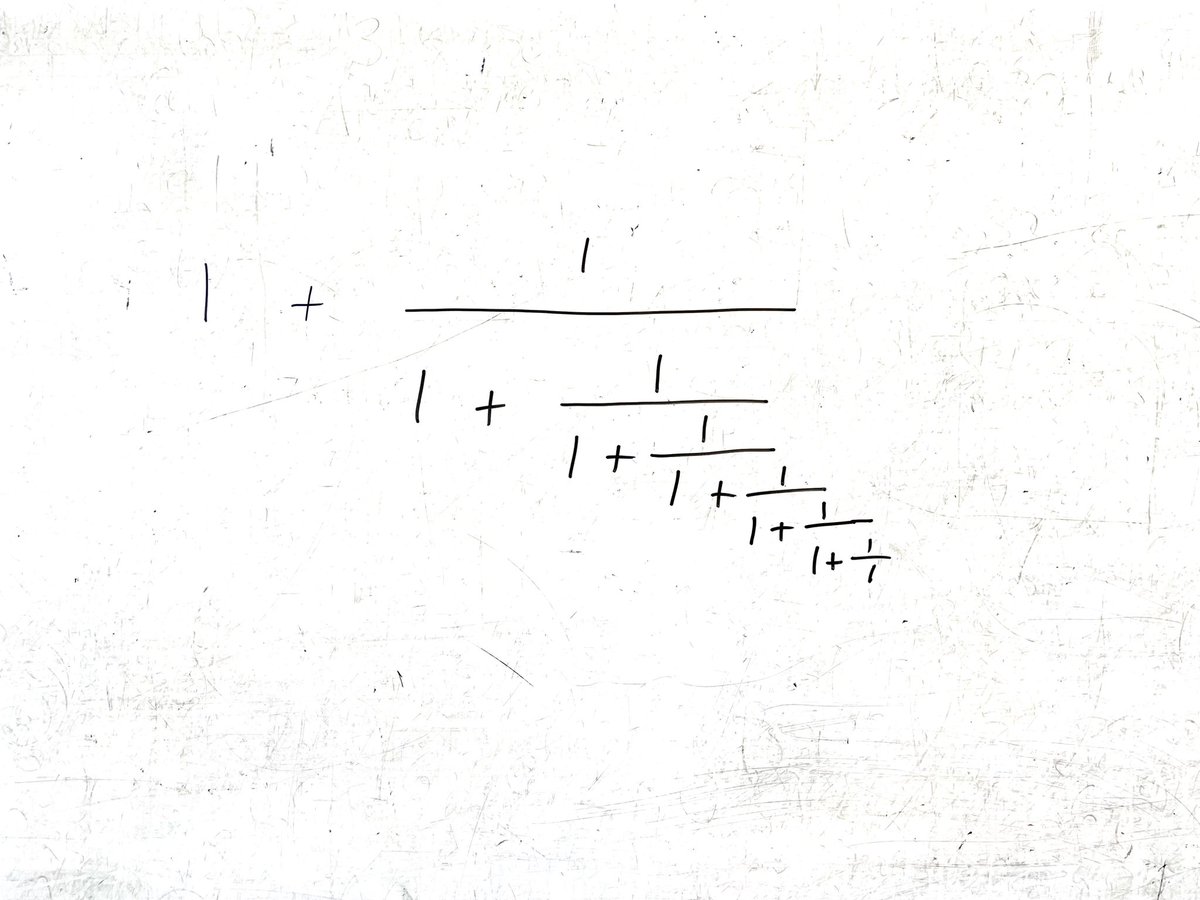
Nearly didn't attempt this with my new S2 last thing today on a baking hot sunny afternoon … but it was worth it. Subtraction as counting-on, place-value mental arithmetic, decomposition awareness … and cognitive load at its limits ;-) Well done S2.
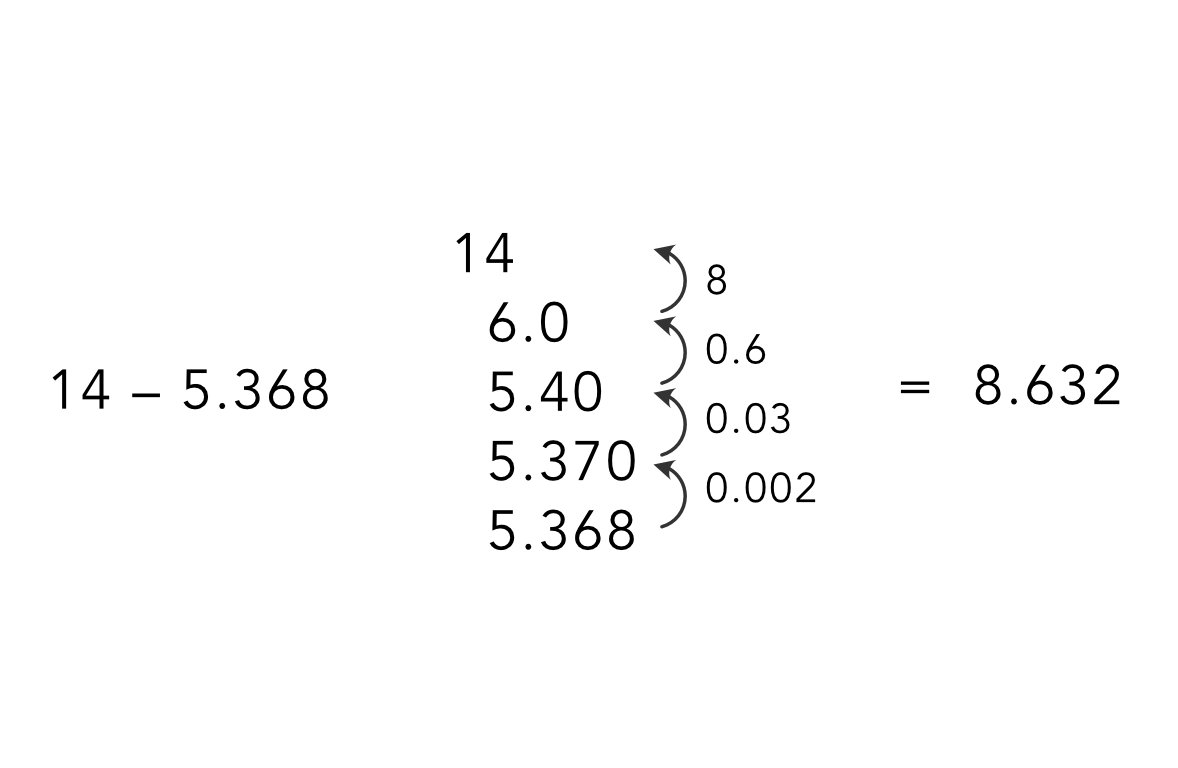
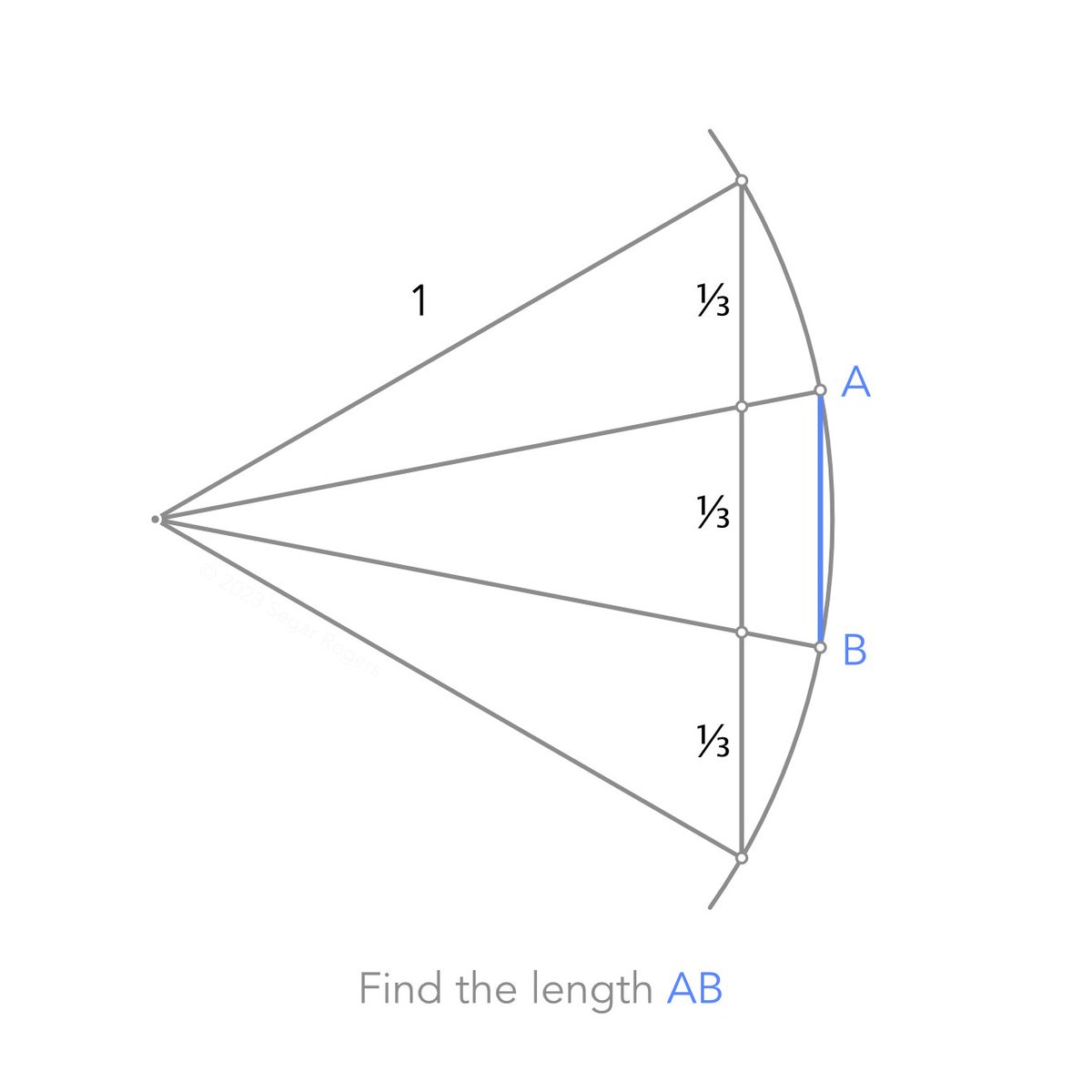
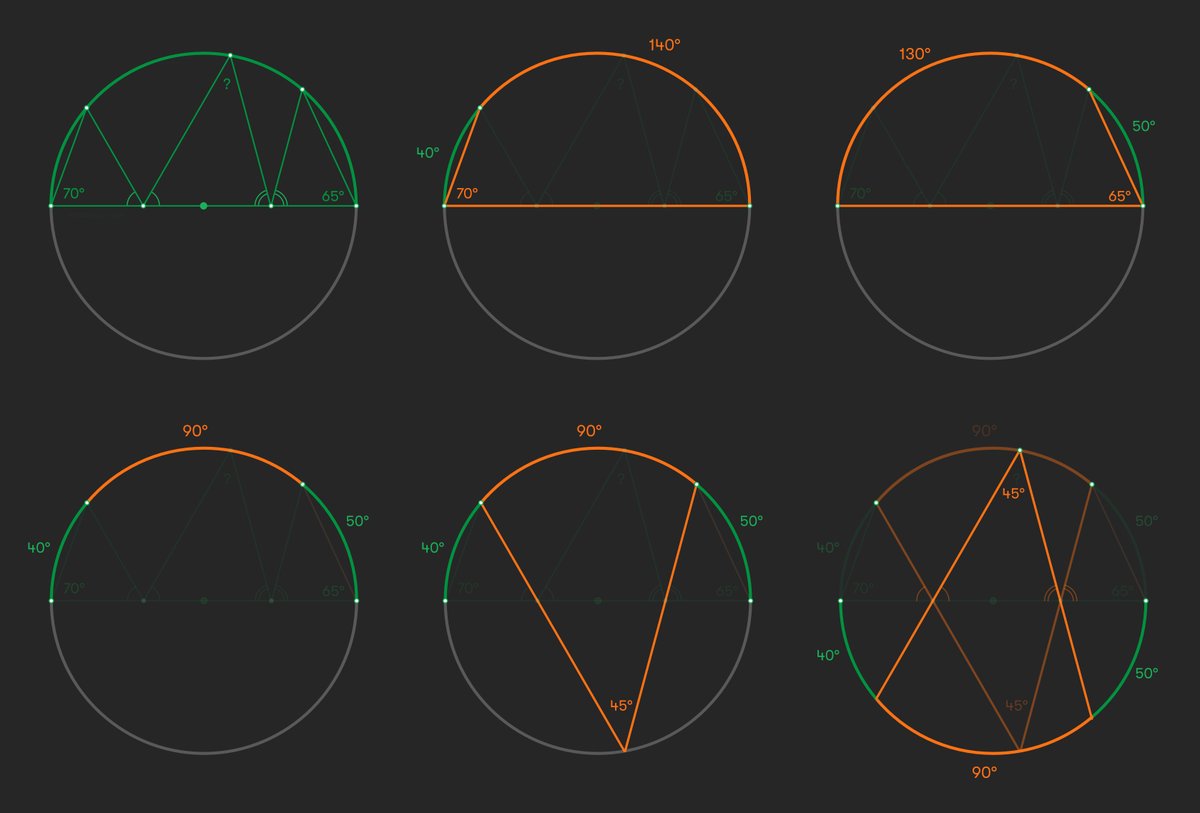
Interesting solutions from: @Mirangu1 @steph_bernard69 @HowTutorial @panlepan @MatthewArcus Here's how I see it. @Cshearer41 @ProfSmudge @suffolkmaths ... angles on the arcs ... trying to convert you ;-)
Inspired by something similar I saw from @edsouthall a while ago. Straightforward ... if you know what you're doing. Don't you hate it when teachers say that ;-)
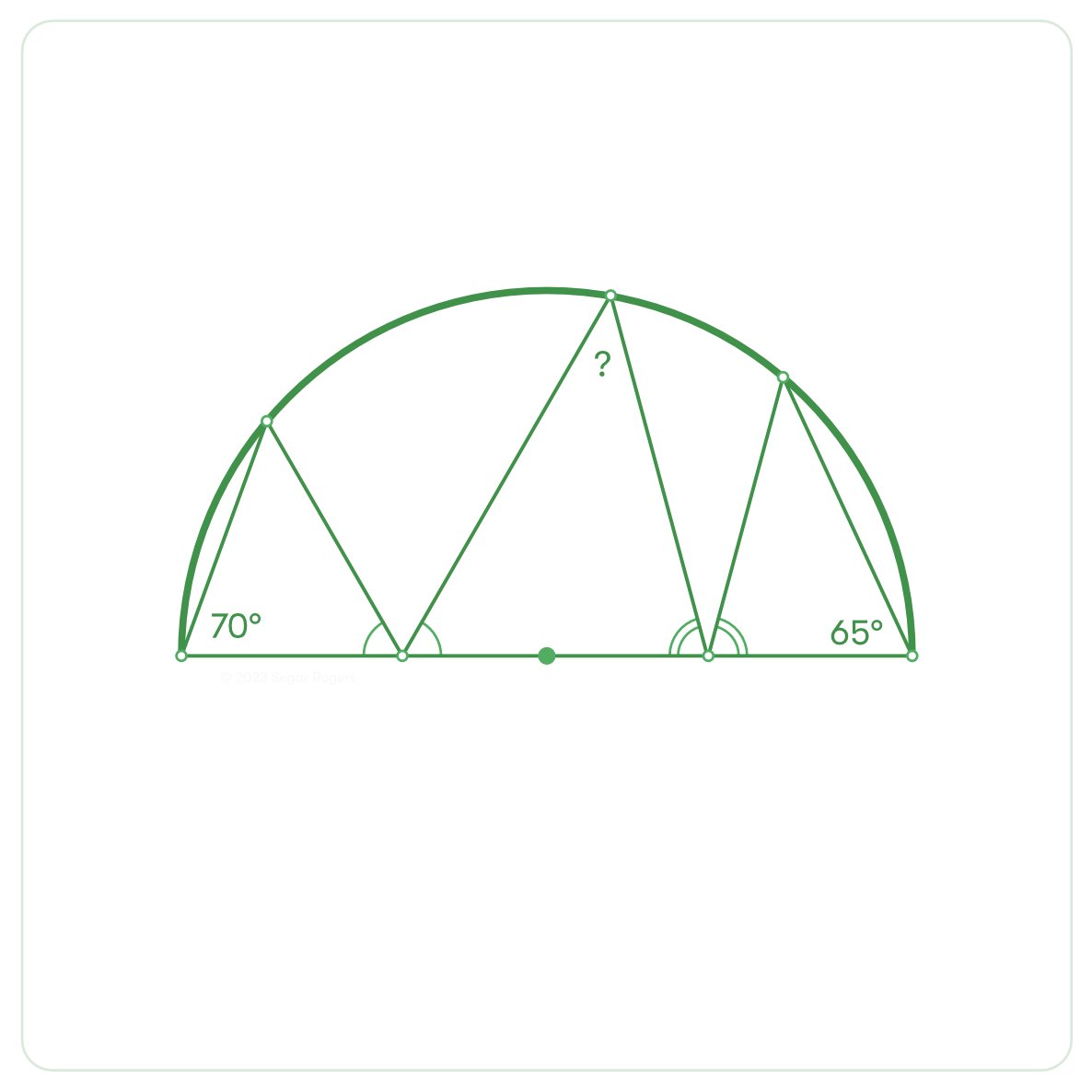
Inspired by something similar I saw from @edsouthall a while ago. Straightforward ... if you know what you're doing. Don't you hate it when teachers say that ;-)

United States Trends
- 1. UConn 9.084 posts
- 2. Dan Hurley 1.530 posts
- 3. Jack Smith 137 B posts
- 4. Solo Ball 1.183 posts
- 5. lana 57,2 B posts
- 6. Tyrese Hunter N/A
- 7. Drake 127 B posts
- 8. Maui 7.615 posts
- 9. Penny Hardaway N/A
- 10. Mahaney N/A
- 11. Kreider 3.946 posts
- 12. Samson Johnson N/A
- 13. COTLTOOZ 1.381 posts
- 14. #ysltrial 4.889 posts
- 15. Newcastle 25 B posts
- 16. Baymax 13,2 B posts
- 17. Harrison Barnes 1.464 posts
- 18. Happy Thanksgiving 16,9 B posts
- 19. West Ham 14,5 B posts
- 20. Judge Chutkan 5.005 posts
Who to follow
-
 Amanda Austin
Amanda Austin
@draustinmaths -
 Rob Southern
Rob Southern
@mrsouthernmaths -
 Chris McGrane
Chris McGrane
@ChrisMcGrane84 -
 Mrs Jagger
Mrs Jagger
@JaggersMaths -
 Paul Rowlandson
Paul Rowlandson
@DrRowlandson -
 White Rose Maths Secondary
White Rose Maths Secondary
@WRMathsSec -
 Amie Meek
Amie Meek
@alcmaths -
 Nathan Day
Nathan Day
@nathanday314 -
 Sam Blatherwick
Sam Blatherwick
@blatherwick_sam -
 Avinash_Math
Avinash_Math
@Avi_Maths -
 Dave Taylor
Dave Taylor
@taylorda01 -
 Jack Brown
Jack Brown
@TLMaths -
 Nicola Waddilove
Nicola Waddilove
@MathsPadNicola -
 Jess Prior
Jess Prior
@FortyNineCubed -
 Mr Hart
Mr Hart
@hartmaths
Something went wrong.
Something went wrong.