大澤裕一
@HirokazuOHSAWA千葉県市川市出身/つくし幼稚園→平田小→市川中・高→東大（理1・理学部数学科）・東大大学院（数理）→SEG・エデュカ/「大学への数学」ほかに連載/高校数学教育（特に統計）の出張研修会を実施/数検1級・統計検定1級合格/趣味はマラソン/14-24かすみがうら,16アクアライン,19,21東京完走/いつか市川に戻りたい/
Similar User
@takechan1414213
@hocsom_sns
@tokyoshuppan
@keisankionwykip
@y_minoda
@g_qjz_taniguchi
@mathelegant
@Go_Nagashima
@4p_t
@yoshihara_math
@sss_education_
@Keio_Sakumon
@f_sei
@884_96
@miumo299792458
大学への数学 2024年10月号（2024/9/20(金)発売）の連載「数学の視野を広げよう！」、今回は極限です。「知りたい量=近似式+誤差」と言う見方と、その極限計算への応用を解説しました。この見方により、ある種の極限計算を、技巧的な計算をせず素直に求められるようになります。ぜひご購読ください！
高校数学に行列・1次変換を戻してください(賛同して戴ける方はリポストをお願いします)。
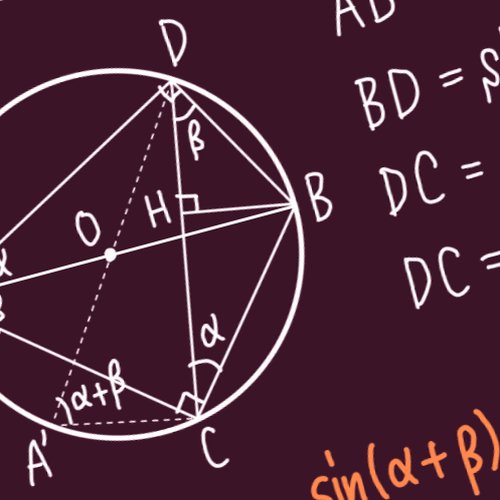
ピタゴラス数の一般形が、単位円周x^2+y^2=1上の点P(0,1)以外の有理点Aとx軸上の有理点Bを「P,A,Bが同一直線上にある」によって一対一対応させて導けるのと同様に、単位球面x^2+y^2+z^2=1上の点P’(0,0,1)以外の有理点A’とxy平面上の有理点B’を同様に一対一対応させることで導けた。 次元を上げてもok.
とても綺麗だ。知らなかった。 ただ、このベクトルは(1,1,-1)方向とのなす角が一定だから、網羅はできないのか。 一般にはどうなのか考えてみたけど、整数a,b,cを使って得られるベクトル(2ac,2bc,a^2+b^2-c^2)の有理数倍で全て得られるかな。大澤先生のは実質c=a+bの場合。
「整数成分の3次元ベクトルで大きさも整数のもの」…☆として(2,2,1)や(6,3,2)は有名ですが,「(1/a,1/b,1/(a+b))(a,bは0以外の整数）の大きさが有理数」を用いれば☆をいくらでも作れます（試してみてください）. ・(1/1,1/3,1/4)//(12,4,3)（大きさ13） ・(1/2,1/3,1/5)//(15,10,6)（大きさ19）など。
Googleドライブの使用率が80%を超えたので、不要なファイルを削除したところ、30GBも減らせた（削除したはずの動画ファイルが何故か色々残っていた）。すっきり。
東工大の幾何学概論の点数 official.kotaroy.com/class/2022/geo… の講義概要より
昔、東大駒場の基礎統計（松原望先生）の授業で、確か試験の点数がx点(0≦x≦100)なら、成績表には10√x点を記録する（例えば試験の点数が36点なら、成績表には60点を記録する）、みたいな話があった（真偽不明）。この変換により点が上がるのはすぐ分かるが、何か理論的な背景がある話なのだろうか？
理論的かどうかはともかく、成績をつけてみるとよくわかりますが、これは直感的にかなり良い感じ（とは）になることが多くて、多少は理由を考えると、正規分布的(?)なのを一様分布っぽく（とは）する感じ（とは）です（※表現は極めて不正確です
昔、東大駒場の基礎統計（松原望先生）の授業で、確か試験の点数がx点(0≦x≦100)なら、成績表には10√x点を記録する（例えば試験の点数が36点なら、成績表には60点を記録する）、みたいな話があった（真偽不明）。この変換により点が上がるのはすぐ分かるが、何か理論的な背景がある話なのだろうか？
昔、東大駒場の基礎統計（松原望先生）の授業で、確か試験の点数がx点(0≦x≦100)なら、成績表には10√x点を記録する（例えば試験の点数が36点なら、成績表には60点を記録する）、みたいな話があった（真偽不明）。この変換により点が上がるのはすぐ分かるが、何か理論的な背景がある話なのだろうか？
「任意の関数f(x)は、偶関数と奇関数の和で表されることを示せ」 ん、「任意の関数」！？ log(x) (x>0) とかは…。
United States Trends
- 1. $CUTO 8.089 posts
- 2. Northwestern 4.578 posts
- 3. Sheppard 2.475 posts
- 4. Denzel Burke N/A
- 5. Jeremiah Smith N/A
- 6. #collegegameday 4.158 posts
- 7. $CATEX N/A
- 8. DeFi 106 B posts
- 9. Broden N/A
- 10. Jim Knowles N/A
- 11. Jahdae Barron N/A
- 12. #Caturday 8.639 posts
- 13. #Buckeyes N/A
- 14. #SkoBuffs 2.249 posts
- 15. Renji 5.120 posts
- 16. Wrigley 2.699 posts
- 17. $XDC N/A
- 18. Henry Silver N/A
- 19. Jack Sawyer N/A
- 20. #MSIxSTALKER2 6.873 posts
Who to follow
-
たけちゃん先生
@takechan1414213 -
安田亨とクリ坊（株式会社ホクソム）
@hocsom_sns -
株式会社 東京出版【公式】
@tokyoshuppan -
佐久間
@keisankionwykip -
蓑田恭秀@鉄緑会
@y_minoda -
谷口貴仁
@g_qjz_taniguchi -
高校数学の美しい物語
@mathelegant -
永島 豪
@Go_Nagashima -
古賀 真輝 『語り合う京大数学』9/18発売
@4p_t -
吉原 修一郎
@yoshihara_math -
SSS Education｜東大理３の教育集団
@sss_education_ -
作問サークル（⊂慶應）
@Keio_Sakumon -
清 史弘 (Fumihiro Sei)
@f_sei -
林 俊介 @ “語り合う京大数学” 重版決定！
@884_96 -
三宅 唯
@miumo299792458
Something went wrong.
Something went wrong.